ch2 - 퍼셉트론 + 자연어 처리 강의

퍼셉트론

---

+) 강의

A perceptron represents a hyperplane decision surface in the ndimensional space of instances

퍼셉트론은 n차원의 좌표평면에서의 초평면 결정면을 나타낸다.

Some sets of examples cannot be separated by any hyperplane, those that can be separated are called linearly separable.

어떤 예시의 셋들은 어떤 초평면으로도 나누어질 수 없는데, 나누어질 수 있는 것들은 선형으로 분리 가능하다고 말한다.

다수의 신호를 입력으로 받아 하나의 신호를 (0 또는 1) 출력

Many Boolean functions can be represented by a perceptron: AND, OR, NAND, NOR

많은 불리언 함수들은 퍼셉트론으로 나타낼 수 있다 : AND, OR, NAND, NOR

XOR: A single perceptron cannot solve such problem

하지만 XOR은 하나의 퍼셉트론으로는 문제를 해결할 수 없다.

XOR is Linearly non-separable

입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치가 곱해진다. 가중치가 클수록 해당 신호가 그만큼 더 중요함을 뜻한다.

뉴런에서 보내온 신호의 총합이 정해진 한계(임계값, theta, θ)를 넘어설 때만 1을 출력한다. ('뉴련을 활성화한다'라고 표현하기도 한다.)

가중치와 편향을 도입한 퍼셉트론의 식

가중치와 편향은 기능이 다르다.

가중치는 각 입력 신호가 결과에 주는 영향력(중요도)을 조절하는 매개변수이고,

편향은 뉴런이 얼마나 쉽게 활성화(결과로 1을 출력)하느냐를 조정하는 매개변수이다.

이 책에서는 문맥에 따라 셋 모두를 가중치라고 할 때도 있다고 한다.

θ를 -b로 치환하여 이항하면 다음과 같다.

논리 회로를 퍼셉트론으로 구현하기

---

1) AND 게이트

 

2) OR 게이트

3) NAND 게이트

XOR 게이트 문제

---

XOR게이트는 배타적 논리합이라는 논리 회로이다. 입력이 모두 1일 때만 1을 출력한다.

 

+강의)

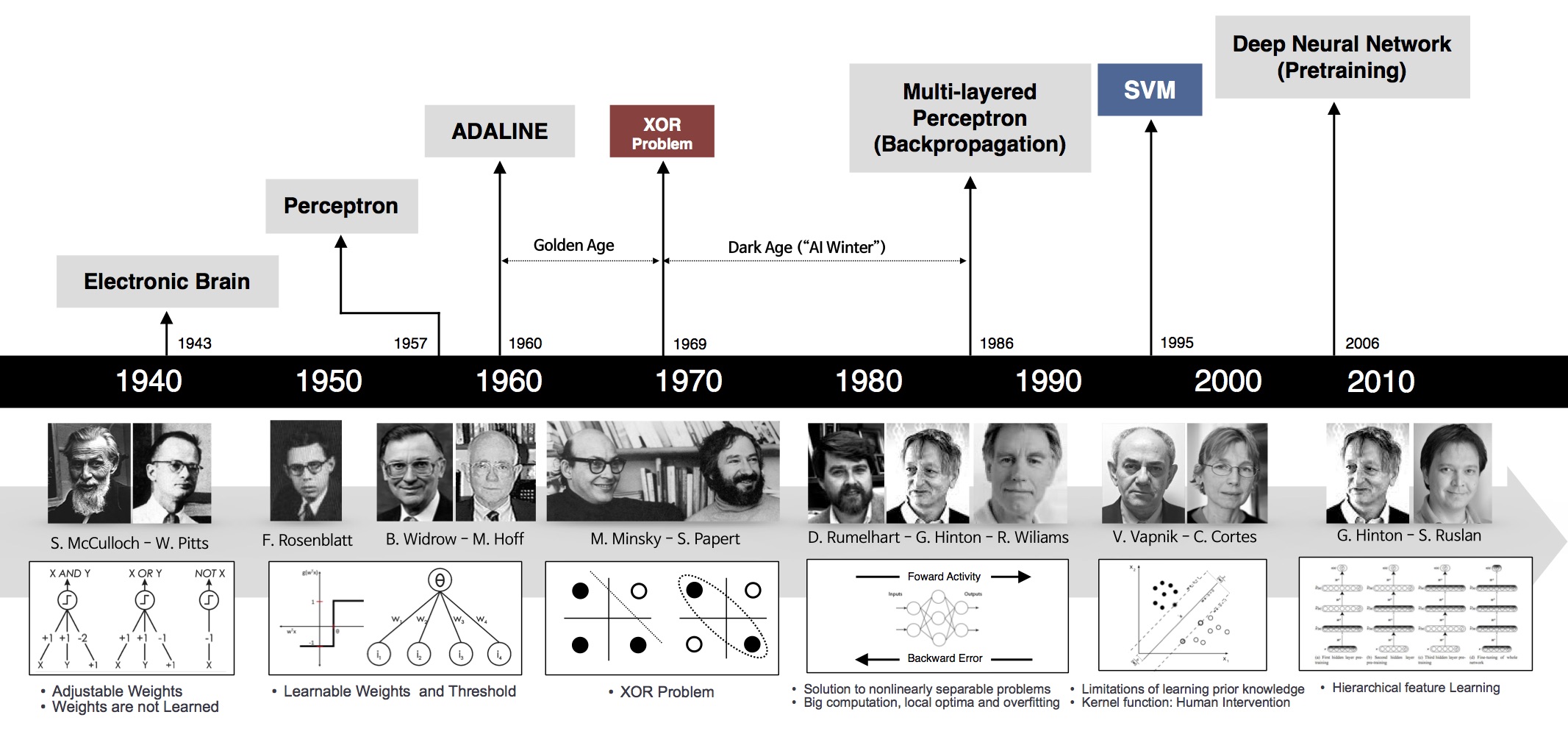
기존의 single perceptron으로는 XOR problem을 해결할 수 없었다.

( 이 문제가 1969년 제기된 이후 약 20년 동안 AI winter라고 불리는 암흑기가 있었다.)

Milestones in the Development of Neural Networks

그런데 직선이라는 제약을 없애게 되면 XOR 문제가 해결 가능해진다. (비선형 영역의 도입)

'비선형'은 퍼셉트론의 '층을 쌓아' 다층 퍼셉트론(multi-layer perceptron)을 만듦으로써 구현 가능하다.

 

NAND와 AND, OR 게이트를 조합해서 NAND 게이트를 구현 가능하다.

입력층 0층, OR, NAND 게이트의 1층, AND 게이트의 2층.

총 2층으로 구성된 다층 퍼셉트론이다.

1) 0층의 두 뉴런이 입력 신호를 받아 1층의 뉴런으로 신호를 보낸다.
2) 1층의 뉴런이 2층의 뉴런으로 신호를 보내고, 2층의 뉴런은 y를 출력한다.

다층 퍼셉트론은 (이론상) 컴퓨터를 표현할 수 있다.

NAND 게이트의 조합만으로도 컴퓨터를 만드는 것이 가능하다.